In this column, I am introducing a novel approach to the mastery of basic facts: the use of higher math to reinforce and practice basic arithmetic. Often the novelty and curiosity of higher math concepts allow basic facts to be practiced in ways that are interesting and even intriguing. One of my favorite such activities with higher math concepts is the investigation of prime numbers.
Briefly, a prime number is a whole number that is divisible by exactly and only two different whole numbers. Thus, 2, 3, 5, and 7 are prime numbers because they can be divided by exactly and only two different numbers - 1 and the number itself.
The numbers 4, 6, and 8 are not prime, because as well as being divisible by themselves and 1, they each are also divisible by 2. The number 9 can be divided by 1 and 9, but it can also be divided by 3, so 9 is not prime. Numbers like 4, 8, and 9 that are divisible by more than 2 whole numbers are called "composite."
The prime numbers less than 200 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, and 199. Refer to this list for later use in the activities described below.
Note three aspects of the list of prime numbers. First, 2 is the only even prime number. Every even number greater than 2 is a composite number. Second, every prime number greater than 2 is an odd number (3, 5, 7, 11, 13, etc.), although not every odd number is prime (9, 15, and 21 are not prime). Third, interestingly enough, the number 1 is not considered prime, simply because it has exactly and only one divisor - the number 1. But 1 is also not considered composite, because composite numbers have 3 or more divisors. Because the number 1 has so many unique properties, we simply put it off in a corner by itself, being neither prime nor composite.
It also helps to think about prime numbers from a multiplication perspective. A number is prime if there are only two different whole numbers that multiply to make that number. The number 13 is prime because 1 and 13 are the only pair of whole numbers that multiply to 13. 29 is prime because 1 and 29 are the only pair of whole numbers that multiply to 29. However, 12 is not prime because 1 and 12 are not the only pair that multiply to 12 (2 and 6 do so, as well as 3 and 4).
Hidden in this multiplication perspective on prime numbers is a valuable insight. If 29 is prime because only 1 and 29 multiply to 29, then this means that no other whole number pairs multiply to 29 - not "7 x 4" or "8 x 3" - none! So if I remember that 4 x 7 is an amount in the 20s - but I cannot remember exactly which number in the 20s - then my familiarity with primes will help me here. Since 29 is prime, then 4 x 7 cannot be 29, since by definition the only pair of whole numbers that multiply to 29 are 1 and 29. Knowing that 29 cannot be the answer to 4 x 7 will reduce the chances of making a mistake like that.
Likewise, knowing that 23 is prime means that whatever 4 x 6 is, it cannot be 23.
But how does one become familiar enough with primes to know that 29 or 23 is prime? Here are several ways.
Prime Numbers and Skip Counting
Skip counting makes a powerful connection with prime numbers. Skip count songs are catchy tunes with fun lyrics in which the chorus is counting by a certain number. For example, a song for 4 could talk about the 4 corners on a table, with the chorus consisting of counting corners on lots of tables, singing, "4, 8, 12, 16, 20, 24, ..." and so on, usually up to 10 times the number, or 40 in this case. Likewise, the "chorus" for 7 would be, "7, 14, 21, 28, 35, 42, 49, 56, 63, 70." The "chorus" for counting by 1 would be the usual "1, 2, 3, 4, 5, . . ."
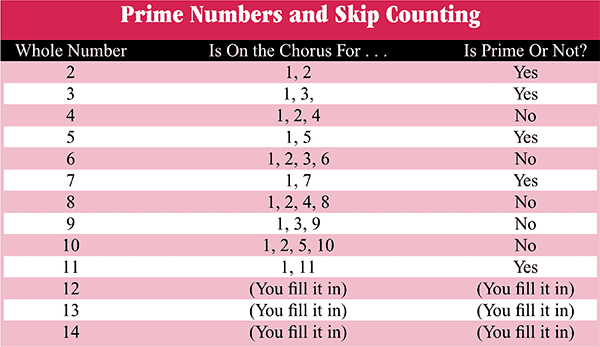
Younger children (ages 5-8) may not understand multiplication or division yet, but they can still be introduced to some pre-multiplication and pre-division explanations of prime numbers. Rather than using the usual definition of prime numbers (whether 8 is divisible only by 1 and 8), we can talk about whether 8 is on the skip count chorus only for 1 and for 8. Of course, every whole number is on the skip count "chorus" for 1 (1, 2, 3, 4, 5, 6, . . . ). If we find that 8 is also on the chorus for numbers like 2, or 3, or 4, etc., then 8 is composite. If 8 is not on any "chorus" except for the chorus for 1 and the chorus for 8, then 8 is prime.
Children can sing the 2s chorus to determine that, yes, 8 is on the 2s chorus ("2, 4, 6, 8, 10, 12"). Therefore, 8 is not prime. Working with the skip count songs, children can discover and fill in information like that shown in Chart 1.
Now let's do a skip count analysis as to whether 11 is prime. Well, 11 is not on the chorus for 2 (2, 4, 6, 8, 10, 12, . . . ), nor for 3 (3, 6, 9, 12, . . . ), nor for 4 (4, 8, 12, . . . ) Neither is 11 on the chorus for 5, for 6, for 7, for 8, for 9, nor for 10.
Since most skip count tapes have songs only through 10, I ask children, "If there were an 11s song, would 11 be on that chorus? [Yes.] Is 11 on the chorus for any other number besides 1 and 11? [No.] If 11 is only on the chorus for 1 and itself, then 11 is prime." Similar explanations can be made for numbers beyond 11.
Corresponding "prime analysis" can be done for any other whole number. For young children in primary grades, be careful about how high to go at first with numbers to be "prime-analyzed" - it does take some time for young kids to work through all the choruses. Although not absolutely necessary, this "prime analysis" is most easily done when children are already familiar with musical skip counting, so acquiring a skip counting tape will really help your child in this and other ways for developing number sense.
Young children (ages 5-8) who are still listening to skip count music tapes might not investigate much beyond the number 20 or 30. Older (ages 7-9) or more mature children could be capable of investigating numbers into the 50s or much higher. In any event, this activity can be meaningful for them at several levels. First, children see that there are lots of patterns in the sequence of whole numbers. Second, children learn to recognize features of that special group of numbers - the primes - that only appear on two choruses. Third, the skip counting analysis provides children with a very informal introduction to division. Finally, kids become familiar with the concept and vocabulary of prime numbers (prime, composite, divisible, multiple).
As an activity, create your own chart with the column headings listed in on page 30 (the numbers in the first column could go as high as you or your child decide). Completing this Prime Number/Skip Counting Chart could be an ongoing activity that is completed over a period of days. In the leftmost column, the boxes with whole numbers that turn out to be prime can be colored one color (maybe pink or purple, for "Prime"), while the composite numbers are colored differently (maybe crimson, for "Composite"). Don't underestimate the power of color as an organizing device that helps store information more effectively in the memory! - "Oh, Dad, that's right - 61 is prime, because I remember 61 is purple."
Summary
Note well that these activities with prime numbers connect higher math with basic arithmetic, producing benefits in both directions. Using these higher math concepts can reinforce and support the practice of basic arithmetic facts, providing one more avenue for the necessary arithmetic practice that is necessary to master basic facts. In the other direction, practicing arithmetic with simple connections to higher math concepts gives children a glimpse or preview of some advanced - and interesting! - topics that are waiting down the mathematical road.
Practicing math facts can be drudgery - as it was for too many of us adults - or it can be intriguing and fun. The wise teacher uses curiosity and novelty to increase learning. Prime numbers are one of several ways to use novelty and curiosity to practice and reinforce basic arithmetic facts. Hooray for prime numbers!
