 In the last issue, I introduced the specific topic of fractions in order
to demonstrate how mathematical principles could be used in this
particular area of math. That demonstration will continue here, focusing
on the Multiple Models Principle and First Name/Last Name Principle.
In the last issue, I introduced the specific topic of fractions in order
to demonstrate how mathematical principles could be used in this
particular area of math. That demonstration will continue here, focusing
on the Multiple Models Principle and First Name/Last Name Principle.
Many Models
Readers may recall a previous article in this column ["Why Manipulatives
Are Not Enough," PHS #16, p. 28] in which the value of using multiple
models was discussed. Here follows the multiple model principle as it
applies to the fraction 34:
- The Real model: a physical, real-world object, such as marking 3
out of 4 equal parts of a length of wood, or eating 3 out of 4 cookies
on the plate.
- The Verbal model: the spoken words "three fourths."
- The Concrete model: math manipulatives, such as fraction tiles (such
as Mortensen Math fraction pieces) in which a transparent square split
into 4 equal parts by black lines is underlaid with 3 colored fractional
segments. (See Figure 1)
- The Pictorial model: sketches, diagrams,
and pictures, such as in Figure 1.
- The Abstract model: the
traditional symbols of math: 3⁄4.
- The
Written model: the written words "three fourths" (distinct from the
spoken word "three fourths").
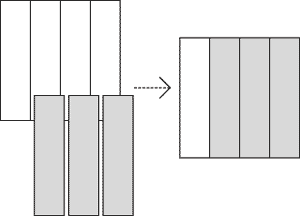
|
|
Figure 1: Using fraction tiles to demonstrate a Pictorial Model of ¾
|
The goal with the use of these multiple models is to have a high degree
of consistency in math between what we say, see, build, write, and draw.
This helps ensure that children receive a fuller, more complete
perspective on the essential elements of what fractions are. Kids learn
that math makes sense.
These connections between and among the various models are related to
issues of learning style. Some children learn most easily with pictures,
so the Pictorial model will be their key that opens the door to
understanding. Other children may find the manipulatives the clearest to
understand (and the most fun, too!), so for them the Concrete model
becomes the foundation upon which the other models are initially built.
Certain children will have little or no problem with the traditional
symbols, so the Abstract model is their strength; but even here,
exposure to other models of math will deepen and enrich these Abstract
learners' understanding and mastery.
 Whatever the preferred model is for an individual child, exposure to
most of the models most of the time (at least in the early years of K-3)
will serve several purposes. First, it can provide variety. Six years of
paper-pencil arithmetic, in my book, can turn off too many students to
the richness and fun of math. Second, this variety of models can also
provide, ironically, continuity and consistency. This continuity arises
from seeing that math now has a high degree of consistency between what
children say, see, build, write, draw, and even sing. Third, familiarity
with most of the models means that if children have a momentary mental
block which keeps them from pulling a particular procedure off the
Abstract hook in their minds, they can fall back on any of several other
solid hooks - the Pictorial hook, the Concrete hook, and so forth.
Whatever the preferred model is for an individual child, exposure to
most of the models most of the time (at least in the early years of K-3)
will serve several purposes. First, it can provide variety. Six years of
paper-pencil arithmetic, in my book, can turn off too many students to
the richness and fun of math. Second, this variety of models can also
provide, ironically, continuity and consistency. This continuity arises
from seeing that math now has a high degree of consistency between what
children say, see, build, write, draw, and even sing. Third, familiarity
with most of the models means that if children have a momentary mental
block which keeps them from pulling a particular procedure off the
Abstract hook in their minds, they can fall back on any of several other
solid hooks - the Pictorial hook, the Concrete hook, and so forth.
Knowing the Names
Another principle of enormous help in the area of fractions is the First
Name/Last Name Principle (FNLN for short). Briefly and broadly stated,
with mathematical quantities, the First Name is the first thing we say,
and the Last Name is the last thing we say. With the fraction
4⁄7, we say "four sevenths." So "four" is
the First Name, and "sevenths" is the Last Name. In other words, the
First Name is the number on top (the numerator), and the Last Name is
the number on the bottom (technically, for most fractions, the Last Name
is the denominator plus the suffix "-ths").
FNLN highlights an important general characteristic of addition and
subtraction that also applies specifically to these two fractional
operations. Examine the following addition exercises in light of FNLN: 2
dogs + 3 dogs = 5 dogs. Notice that when adding things that already have
the same Last Name ("2 dogs + 3 dogs"), the answer combines the First
Names by addition (the "5" came from "2 + 3") but it keeps the same Last
Name ("5 dogs"). By counterexample, we do not say "2 dogs + 3 dogs = 5
dogs dogs" (where the Last Name is shown twice). Properly, with addition
and subtraction of quantities already having the same Last Name, the
answer keeps that same Last Name. This holds true regardless of the last
name: 2 ft2 + 3 ft2 = 5 ft2; 2x + 3x = 5x; or 2 hundred + 3 hundred = 5
hundred.
For example, in the fraction addition problem of 2⁄7 + 3⁄7, both
fractions already have the same Last Name ("sevenths"), so their sum
should keep that Last Name of "sevenths," yielding 2⁄7 + 3⁄7 = 5⁄7.
Understanding FNLN helps children avoid the very common mistake with
fraction addition, that 2⁄7 + 3⁄7 = 5⁄14 (which, of course, it doesn't).
This aspect of FNLN applies to subtraction, too. This FNLN principle
holds across mathematical topics, and it's a great example of how using
proper principles can keep mathematics simple.
The FNLN principle also incorporates the fact that all quantities have
more than one First Name/Last Name label. Next issue, we will examine
how this applies to adding or subtracting fractions that have different
Last Names, such as 2⁄7 + 1⁄4.
Bob Hazen is a proud father of two sons who are homeschooled mostly by
his wife, Sarah. He has taught math in the St. Paul, Minnesota, public
schools since 1988, and is on the adjunct faculty at Augsburg College.
He was director of the Chelsea Project, in which algebra, calculus,
music, and manipulatives were used to teach math to regular first-grade
students in a traditional school setting. Since 1995, he and Sarah have
operated the Summer Algebra Institute for Kids (for grades 1-4), the
goal of which is to use music and hands-on algebra to turn students on
to math.