Lies, Part II: The Importance of Consistent Verbalizations
By Bob Hazen
Printed in Practical Homeschooling #18, 1997.
 How to make our mathematical verbalizations both accurate and consistent!
How to make our mathematical verbalizations both accurate and consistent!

|
 |
 Verbalizations are translations into or from the Verbal model (i.e. spoken words) - whether paired with Abstract symbols, Concrete manipulatives, or Pictorial sketches. In the last issue I claimed that certain mathematical verbalizations are lies. By lies, I mean statements that are sometimes simply wrong or, more often, only true within a very limited context. Our verbal explanations need to be both accurate to the mathematical facts, concepts, and activities they are describing while also being consistent with other modalities and with other math topics in later grades.
Verbalizations are translations into or from the Verbal model (i.e. spoken words) - whether paired with Abstract symbols, Concrete manipulatives, or Pictorial sketches. In the last issue I claimed that certain mathematical verbalizations are lies. By lies, I mean statements that are sometimes simply wrong or, more often, only true within a very limited context. Our verbal explanations need to be both accurate to the mathematical facts, concepts, and activities they are describing while also being consistent with other modalities and with other math topics in later grades.
Part I of this article dealt with three examples of using carefully crafted verbal explanations. The words we use (the Verbal mode) should be consistent with the symbols (the Abstract mode), the manipulatives (the Concrete mode), and the sketches (the Pictorial mode) that our children also work with. This connection works both ways: when there is consistency among these modes, our children learn more effectively. When there is inconsistency or contradiction among these modes, kids get confused and frustrated. One way to think of this as a goal is to make math become as simple as, "Say what you see, write what you say."
The lies dealt with in this article are primarily addressed to the teaching of young children (kindergarten through grade 3 or 4). Regrettably, the insights here might be raised too late for older children. They may already have acquired the confusion that contributes to math phobia.
Example #4
The Lie: For two-digit numbers between 9 and 20, we usually verbalize, for example, the symbols "14" as "fourteen."
The Problem: Our English words for numbers in the teens don't reinforce place value. Unlike most two-digit numbers, the first ten numbers that our kids encounter after 9 do not have good consistency between the symbols we write from left to right and the corresponding words we say from first to last. By the time young children "get to" the more regularly worded amounts from 20 to 99, the potential for confusion has been established.
The Confusion Now: For the most part (but with notable exceptions), two-digit base ten numbers comply with the following "verbal formula":
Say the tens digit, then say the letter "T," then say the ones digit (unless the ones digit is zero, in which case we say nothing).
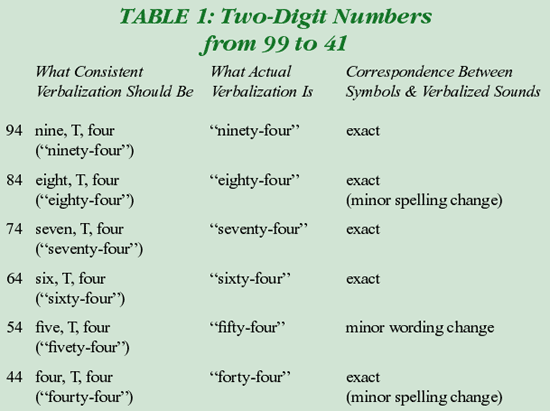
For example, the number "94" means "9 tens, 4 ones," and the sounds we make for the symbols "94" are, "nine, T, four." In this case, the order of the spoken sounds from first to last matches the order of symbols from left to right (with the T corresponding, if we wish, to an abbreviation for "tens"). The degree of this consistency in the sequence of numbers in Table 1 comes across much better if you read all the numbers aloud (see "Table 1").
Notice how from 99 down to 41, the English verbalization of the numerical symbols is essentially consistent with this formula of "tens digit, T, ones digit." Hearing the symbols "94" being verbalized as the sounds "nine T, four" connects with the genius of the base ten place value system - each place has a different value. In base ten, those values are each based on consecutive powers of 10. From "nine T, nine" down to "four T, one," we are using sounds (and written words) that reinforce place value. In other words, there is a high degree of consistency between what we say, see, and write. This intermodal consistency helps students understand the meaning and value of our base ten symbol system. However, look what happens in Table 2 - here is where we start to have some fun (especially if you read this aloud) (see "Table 2").
Even in the 20's, the actual verbalized sound "twenty-four" isn't too far from what would be the consistent "tens digit, T, ones digit" verbalization of the amusing "twoty-four." In all these numbers from the 90's to the 20's, the words we say (and words we write) from left to right correspond with reasonable consistency to the symbols we write from left to right.
When we now drop below 20, things gets funnier to the ear - notice the major change in the verbalized order of the digits in English when we say the words for the symbols "14" (see "Table 3" on the following page).
In the teens, the order of the verbalization doesn't match the order of the symbols. For the symbols "14," our normal English has us say "ones digit, teen" - "fourteen." (For 10, 11, and 12, there is almost no correspondence between the symbols and the words.)

The Truth: For young children (pre-K to grade 2) who are beginning to learn number names, I extend the truthful formula "tens digit, T, ones digit" to all two-digit numbers. I simply teach them two names for the digits in the teens. First, we examine (as above) how the numbers from, say, 94 down to 44 are consistently worded to remind us about place value order.
After this, I lead them down through the numbers below 40 with this type of explanation:
- "34" we usually say as "thirty-four," but it should be "threety-four" [giggles]. We'll use either name when we verbalize the symbols "34."
- "24" we say as "twenty-four," but it should be "twoty-four" [laughter]. We'll use both names for "24" also.
- "14" we say as "fourteen," but it should be "onety-four" [more laughter]. So "14" also has two names.
- How should we say the symbols "17"? That's right, it should be "onety-seven," but its usual name is "seventeen." That funny name "onety-seven" is going to be our secret name for the symbols "17." You'll hear me use both names, and I want you to use both names, too.
- Okay, let's count up from 8: eight, nine, onety, onety-one, onety-two, onety-three, onety-four, onety-five. . .

Children love secrets, and I tell them that most other kids and adults won't ever have heard of the name "onety-seven." But I also prepare them for other people who will try to correct them and say, "No, you should say "seventeen."
I tell my kids to just smile and remember that it's our secret name for that kind of number.
Example #5
The Lie: The fraction symbols of "1/2" is usually verbalized as "one-half." A lesser inconsistency is verbalizing "1/3" as "one-third."
The Problem: The names for fractions with a 3 or a 2 on the bottom have little or no verbal correspondence to their respective numerals "three" and "two."
The Why: For most fractions, the names we say for the symbols comply with the following verbal formula: say the top number, then say the bottom number, then add the sound of "-ths." For example, for the fraction symbols 4/9, the formula dictates we should say "four, nine, -ths" - which is exactly the sound we make: "four ninths." Likewise for 7/10 - "seven, ten, -ths" - again, just like the sounds we say: "seven tenths." Most fractions with denominators of 4 or more have a high degree of consistency between the symbols we see and the words we say.
The Truth: I extend the truthful formula "top number, bottom number, -ths" to all fractions, with some humorous and memorable results. Like having two names for numbers in the teens, I simply teach them two names for fractions with a 2 or a 3 on the bottom:
- For the fraction 2/3, the symbols should be verbalized as "two threeths" [giggles], although we usually say "two thirds." We'll use both names.
- For the fraction 1/2, the symbols should be verbalized as "one twoth" [much laughter], although we usually say "one half." You can remember both names, can't you?
- How should we say the fraction 3/2 if we were consistent? Should it be "three twoths" - or should it be "three teeth"? [howls of laughter; consistent verbalizations can be fun!]
Some readers may think that this is being too picky. After all, learning "one half" for "1/2" is not a big deal, is it? Yet, that's the whole point: verbalizing "1/2" as "one half" is not a big deal per se. The real problem is that there are dozens of such inconsistencies in math between what we say, see, build, write, and draw. Individually, each inconsistency is "no big deal." However, these dozens of inconsistencies are compounded by thousands of encounters in math where what is written is not the same as what is said. The cumulative effect of all those inconsistencies (between what kids say, see, build, write, and draw) is that students too often conclude with some justifiable logic, "Math just doesn't make sense."
We achieve consistency by practicing consistency, one case after another after another. Verbalizing "13" as "onety-three" may be one silly example. But these consistent verbalizations help foster our goal: understanding, enjoyment, and competence in mathematics.